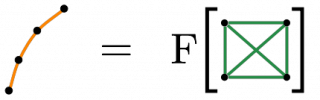
Synopsis
We consider the problem of clustering in domains where the affinity relations are not dyadic (pairwise), but rather triadic, tetradic or higher. The problem is an instance of the hypergraph partitioning problem. We propose a two-step algorithm for solving this problem. In the first step we use a novel scheme to approximate the hypergraph using a weighted graph. In the second step a spectral partitioning algorithm is used to partition the vertices of this graph. The algorithm is capable of handling hyperedges of all orders including order two, thus incorporating information of all orders simultaneously. We present a theoretical analysis that relates our algorithm to an existing hypergraph partitioning algorithm and explain the reasons for its superior performance. We report the performance of our algorithm on a variety of computer vision problems and compare it to several existing hypergraph partitioning algorithms.
Project Details
Non UCSD Vision People also Involved
Lihi Zelnik-Manor and Pietro Perona (Caltech)
Jongwoo Lim (UIUC)
